Le test ANOVA : comprendre l’analyse de la variance
L’ANOVA est un outil statistique permettant d’identifier si des différences significatives existent entre plusieurs groupes. Que ce soit dans les domaines de la santé, en sciences sociales, en marketing ou encore en ingénierie, ce test est essentiel pour comprendre l’impact de certains facteurs sur une variable donnée. Comment fonctionne-t-il ? Quels sont ses différentes spécificités et comment les utiliser efficacement.
Nous allons répondre à ces questions dans cet article !
Qu’est-ce que le test ANOVA ?
L’analyse ANOVA permet de comparer les moyennes de plusieurs groupes dans le but de définir l’existence de différences significatives entre eux. En effet, elle repose sur l’hypothèse nulle (H₀) selon laquelle toutes les moyennes des groupes sont égales. Si au moins une des moyennes est différentes, on parle alors d’hypothèse alternative (H₁).
Lorsqu’une hypothèse alternative se vérifie, on dit alors que le test est significatif. Cependant, bien qu’elle détermine quel groupe a une moyenne différente des autres, cette étude statistique ne nous laisse pas pour autant savoir lequel. Il convient alors de réaliser des tests post-hoc afin de l’identifier.
À savoir : Le modèle ANOVA est fréquemment confondu avec un t-test ou avec un test omnibus, pour les plus connaisseurs. Il est vrai que ces tests sont corrélés d’une certaine manière, pourtant, ils n’en restent pas moins différents :
- Le test omnibus est le terme générique donné aux tests statistiques qui vérifient une différence globale entre plusieurs groupes. Cette méthode permet de tester une hypothèse générale. (ANOVA = test omnibus).
- Le t-test, aussi appelé test de Student, confronte uniquement deux groupes pour voir si leurs moyennes sont significativement différentes. Il n’est cependant pas considéré comme un test omnibus, car il ne teste qu’une seule comparaison entre deux groupes et ne s’applique pas aux analyses globales sur plusieurs groupes.
- L’ANOVA, quant à lui, compare trois groupes ou plus afin de déterminer si leurs moyennes sont significativement différentes. Il existe plusieurs types de modèles ANOVA que nous détaillons ci-dessous.
Les différents types d’ANOVA expliqués
Pour utiliser l’ANOVA, il convient d’utiliser une variable quantitative qu’il suffit de mettre en relation avec une ou deux variables qualitatives. Ces dernières sont des variables catégorielles aussi nommées « facteurs de variabilité » et sont les éléments déclencheurs d’une méthode d’application spécifique de l’ANOVA. On dénombre 4 méthodes distinctes à partir de ces facteurs :

Réaliser une analyse de variance avec Selvitys

L’ANOVA unifactorielle
Ce test permet de comparer les moyennes de trois groupes ou plus sur une seule variable indépendante (facteur).
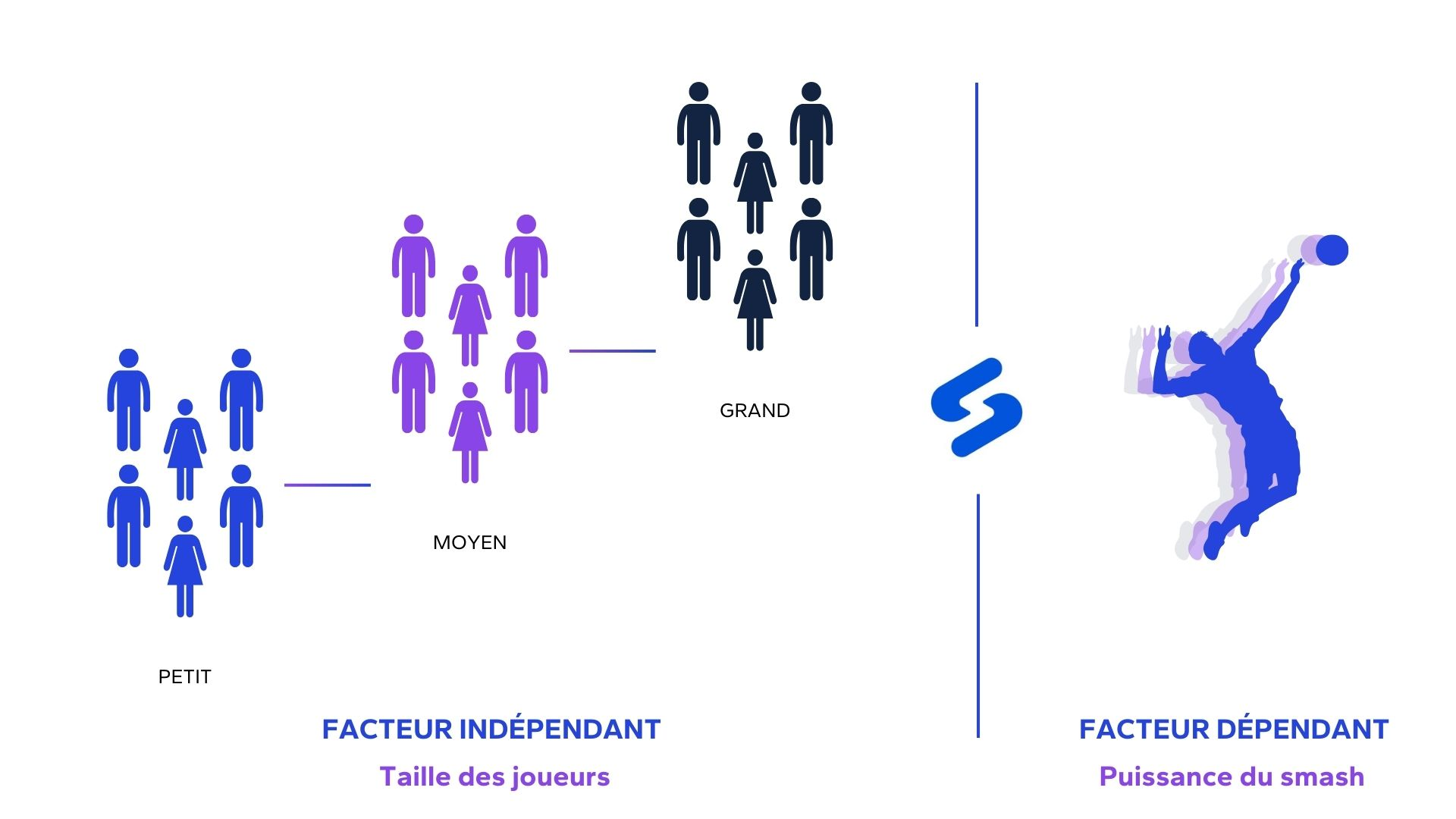
Prenons un exemple concret. Nous cherchons à savoir si, au volley, la taille des joueurs est un facteur qui influence la puissance du smash. Dans ce cas, il convient de se poser la problématique suivante :
La taille influence-t-elle la puissance d’un smash au volley ?
Notre variable indépendante (facteur) est la taille des joueurs. Elle se divise en trois catégories : petit, moyen, grand.
Notre variable dépendante est la puissance du smash, que l’on calcule en km/h.
Ainsi qu’une hypothèse alternative H₁ : Au moins un groupe présente une puissance de smash différente des autres.
Il est désormais possible d’effectuer notre test. Nous évaluons la puissance de smash de chaque catégorie (petit, moyen et grand) puis nous appliquons une ANOVA unifactorielle via le logiciel SPSS, Python, R ou Excel.
Enfin, nous interprétons les résultats et vérifions nos hypothèses :
- Si l’ANOVA est non significative, notre hypothèse nulle est vérifiée → La taille n’influence pas la puissance du smash.
- Si l’ANOVA est significative, notre hypothèse alternative est vérifiée→ La taille joue un rôle, et on doit identifier quelles catégories sont différentes.

L’ANOVA à deux facteurs
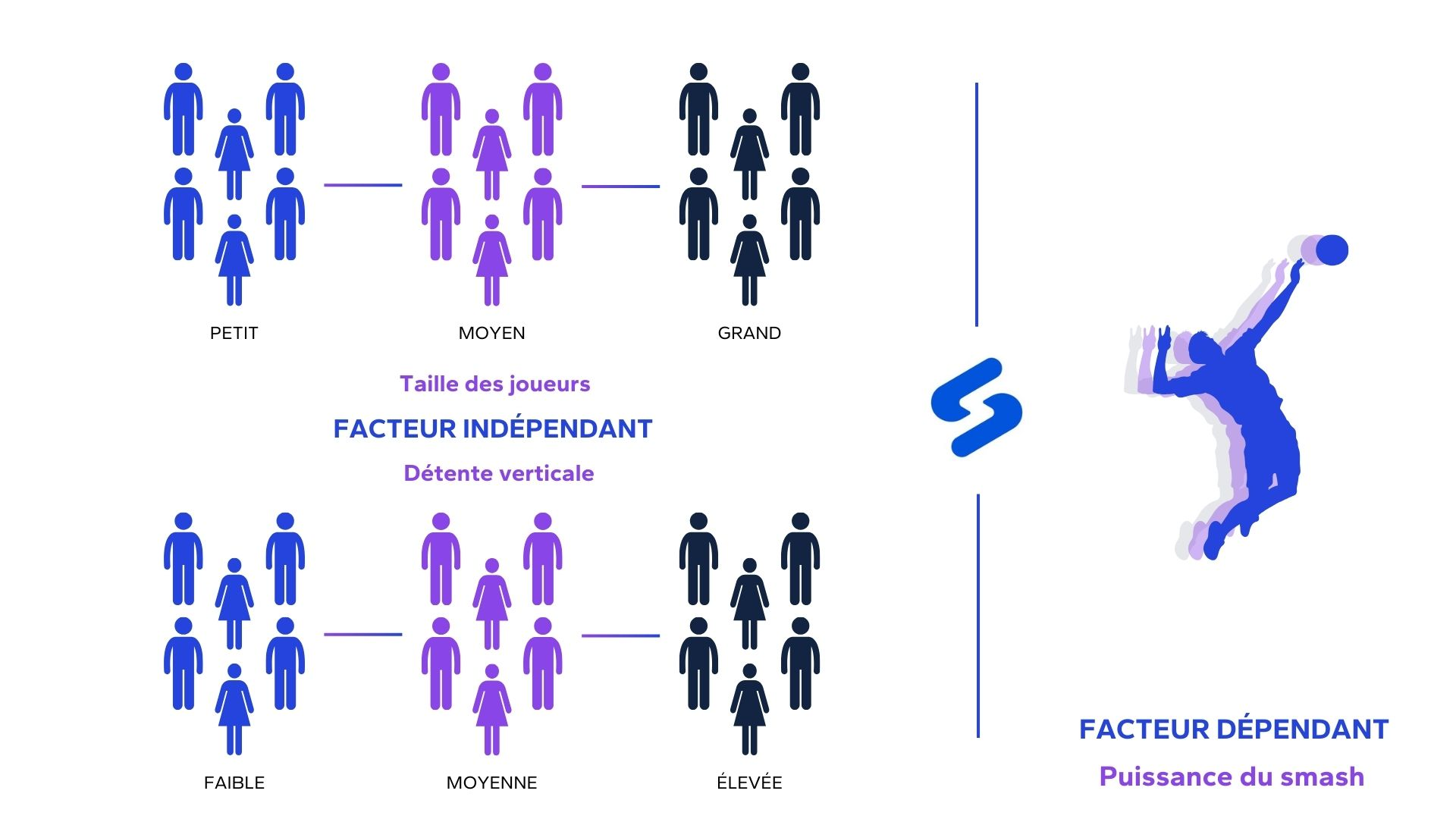
Reprenons notre exemple précédent. Ici, nous cherchons à analyser l’effet combiné de la taille et de la détente verticale sur la puissance du smash. Nous déterminons la problématique suivante :
La taille et la détente verticale influencent-elles la puissance d’un smash au volley ?
Pour cette expérience, nous avons deux facteurs indépendants
- La taille des joueurs divisée en trois catégories (petit, moyen, grand).
- La détente verticale divisée en trois catégories (faible, moyenne, élevée).
Notre variable dépendante n’a pas changé. Il s’agit de la puissance du smash, que l’on calcule en km/h.
Une hypothèse alternative H₁ : Au moins un des facteurs a un effet significatif.
Lors de notre test, nous mesurons la puissance du smash pour des joueurs de différentes tailles et ayant des détentes verticales différentes. Nous appliquons ensuite une ANOVA à deux facteurs pour analyser :
- L’effet de la taille seule.
- L’effet de la détente seule.
- L’interaction entre taille et détente (par exemple : les grands joueurs bénéficient-ils plus d’une bonne détente que les petits ou les moyens ?).
Suite à une interprétation des résultats, nous vérifions nos hypothèses :
- Si l’ANOVA est non significative, notre hypothèse nulle est vérifiée → Ni la taille, ni la détente verticale n’influencent la puissance du smash.
- Si taille et détente sont significatives, notre hypothèse alternative est vérifiée → Ces deux facteurs influencent la puissance du smash.
- Si l’interaction entre variables indépendantes est significative → L’effet de la taille dépend du niveau de détente verticale (par exemple. : un grand joueur avec une forte détente a un avantage encore plus marqué).

L’ANOVA à mesures répétées
Pour un facteur
Cette méthode s’utilise lorsque les mêmes échantillons sont évalués plusieurs fois dans des conditions différentes. Contrairement à une ANOVA classique où chaque mesure est indépendante, ici, chaque individu est testé à plusieurs reprises, ce qui permet de mieux contrôler la variabilité individuelle.
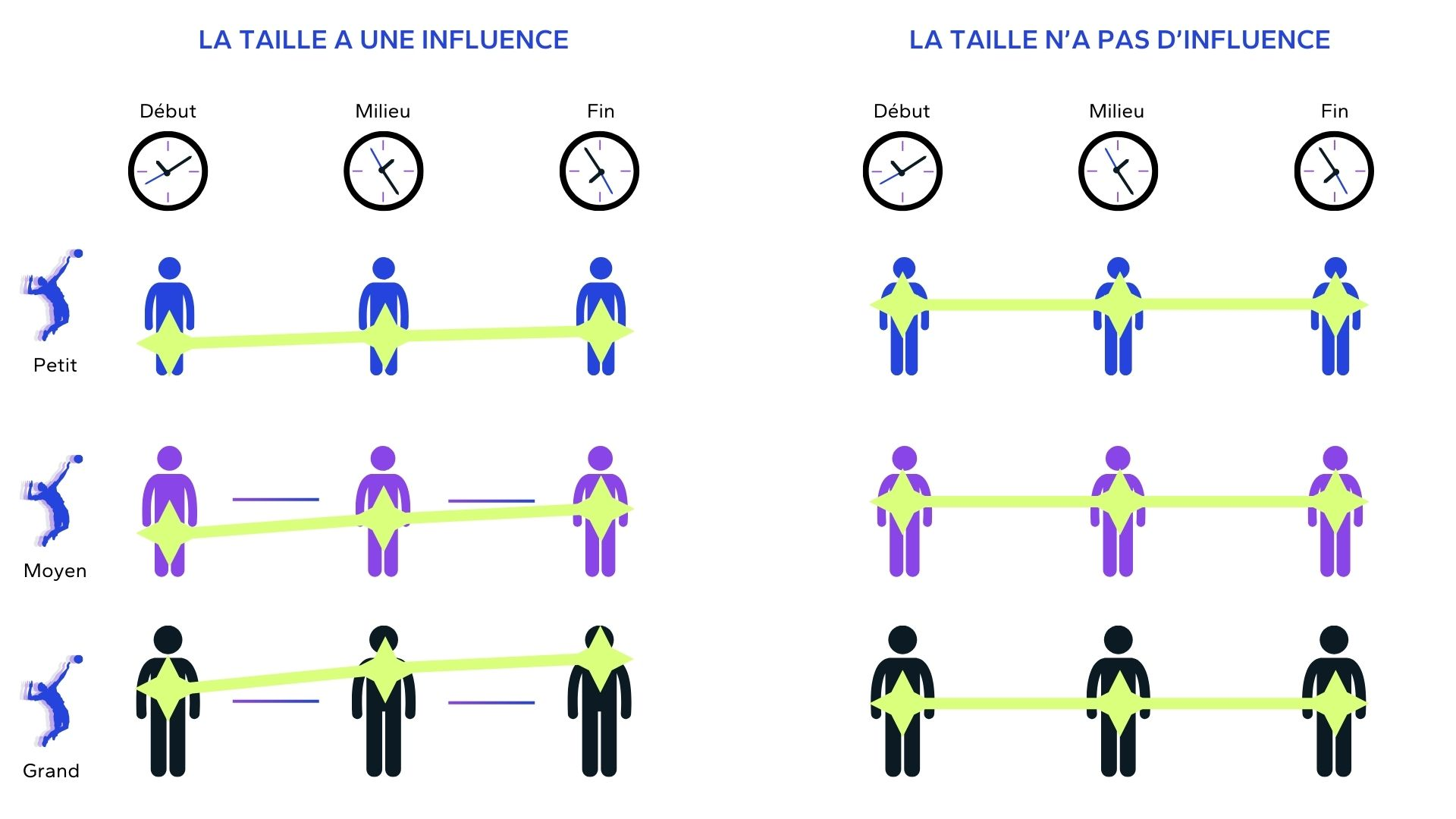
Prenons l’exemple de 3 joueurs de volley (petit, moyen et grand) où nous cherchons à savoir si la taille influence la puissance du smash au fil d’un match. Pour ce faire, nous mesurons la puissance moyenne des smashes (en km/h) du joueur petit, moyen et grand à trois moments clés : au début, au milieu et à la fin du match.
Cet exemple étant fictif, imaginons que pour chaque joueur, nous obtenions les résultats suivants :
| Joueurs | Début du match (km/h) | Milieu du match (km/h) | Fin du match (km/h) |
|---|---|---|---|
| 1 | 85 km/h | 87 km/h | 88 km/h |
| 2 | 90 km/h | 93 km/h | 95 km/h |
| 3 | 95 km/h | 98 km/h | 100 km/h |
Exemple dans le cas d’une hypothèse alternative : le test est significatif.
Grâce au tableau ci-dessus, nous pouvons observer les résultats suivants :
- Les joueurs petits semblent avoir une puissance de smash relativement stable avec une légère augmentation (+3 km/h sur tout le match).
- Les joueurs moyens montrent une amélioration plus marquée (+5 km/h).
- Les grands joueurs affichent la même progression (+5 km/h), et globalement la plus grande puissance de smash dès le début.
Ces valeurs nous permettent donc de tester :
- L’effet du temps (est-ce que la puissance du smash augmente au cours du match ?)
- L’effet de la taille du joueur (est-ce que la taille influence la puissance du smash ?)
- L’interaction entre temps et taille (est-ce que l’évolution de la puissance dépend de la taille ?)
Évidemment, un ANOVA vous permettra de réaliser ce type d’opérations sur des données bien plus conséquentes. L’exemple ci-dessus ne sert uniquement d’exemple et ne représente pas la réalité. En effet, il est conseillé d’utiliser des logiciels tels que SPSS, R ou Python pour réaliser un ANOVA plus complet.
Pour deux facteurs
Dans le cadre d’une analyse à deux facteurs, nous examinons l’effet combiné de deux facteurs sur les mêmes échantillons, tout en appliquant des mesures répétées sur l’un ou les deux facteurs. Ajoutons à notre exemple précédent, la détente verticale comme second facteur. Nous avons alors des joueurs de volley de différentes tailles (facteur 1) et avec différentes détentes verticales (facteur 2). Chaque facteur est mesuré à plusieurs moments durant le match. L’objectif est toujours de comprendre si la progression de la puissance du smash varie en fonction de la taille des joueurs à différentes périodes du match, soit au début, au milieu et à la fin. Tout en mesurant l’influence de la détente verticale sur ces mêmes périodes (début, milieu et fin).
En conclusion
L’ANOVA à mesures répétées est particulièrement utile pour analyser l’évolution d’une ou plusieurs variables dans le temps ou sous différentes conditions, tout en prenant en compte les caractéristiques propres à chaque individu.
À savoir : En tant qu’institut de sondage, Selvitys peut vous accompagner dans la réalisation de ce test, notamment pour des études sur la perception des prix ou la satisfaction client. Par exemple, nous pouvons analyser comment le prix d’un produit ou d’un service évolue ou encore mesurer l’évolution de la satisfaction après plusieurs interactions avec une entreprise.

Réaliser une analyse de variance avec Selvitys

Réaliser une analyse de variance avec Selvitys
Les limites de l’ANOVA
Comme nous l’avons mentionné plus tôt, l’une des spécificités de l’ANOVA réside dans son imprécision. En effet, bien qu’elle permette d’analyser la différence moyenne entre plusieurs variables indépendantes, elle n’indique pas lesquelles d’entre elles sont différentes.
Pour palier à ce problème, il est nécessaire de réaliser une seconde analyse statistique, appelée post-hoc. Pour citer certaines de ces méthodes, vous pouvez utiliser les étendues de Tukey, la correction de Bonferroni ou les contrastes de Scheffé. Ces méthodes vous permettent d’effectuer une comparaison multiple en une seule étape afin de définir les groupes qui sont différents dans votre ANOVA.
Utiliser l’ANOVA sur un petit échantillon
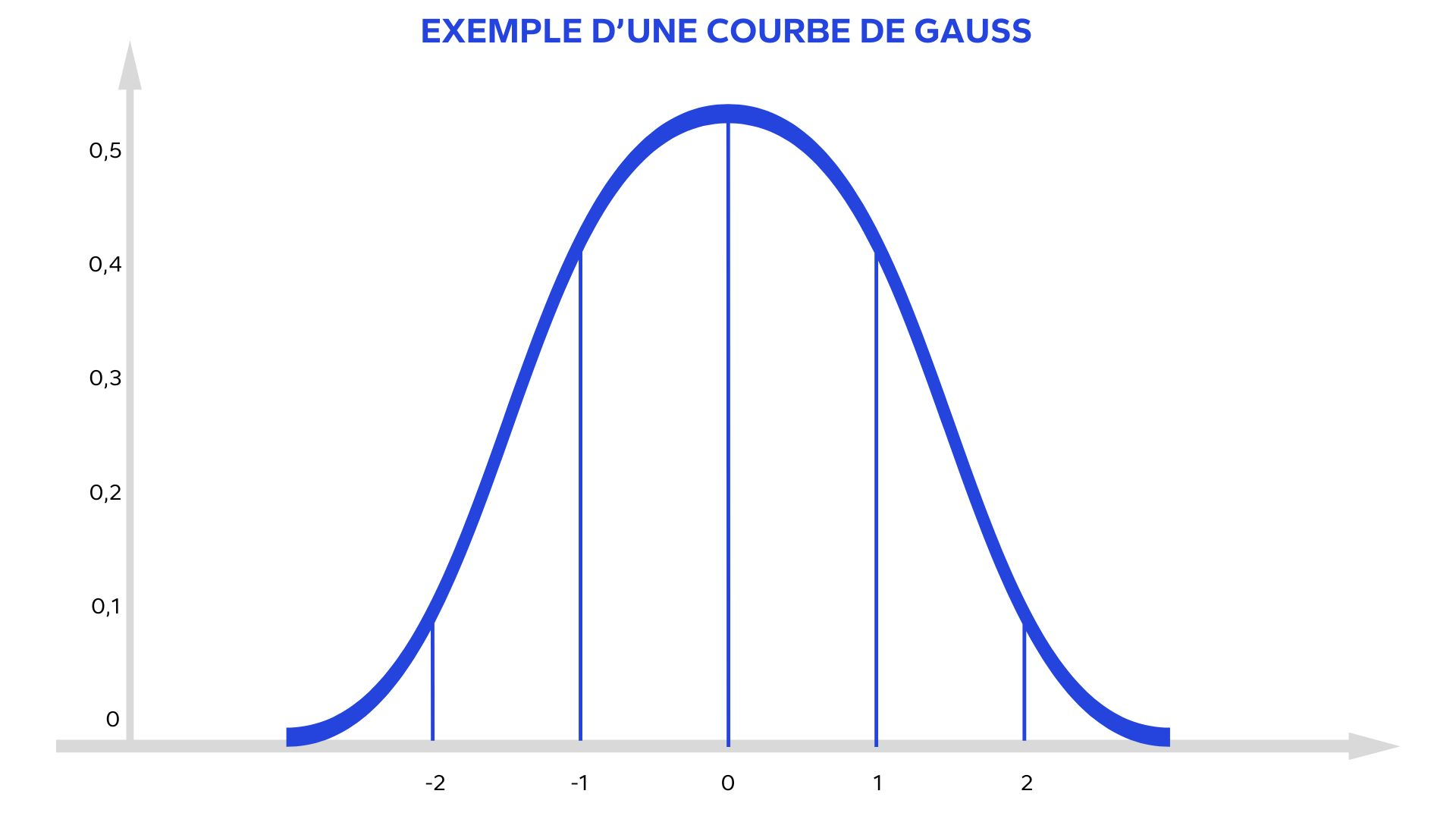
Il est essentiel de s’assurer qu’un échantillon restreint suit une distribution normale avant toute analyse. Une distribution est dite normale lorsqu’elle adopte une forme en cloche parfaitement symétrique autour de la moyenne, ce qui implique que la moitié des valeurs se situent au-dessus et l’autre moitié en dessous. C’est le concept de la courbe de Gauss.
Une ANOVA, tout comme un t-test, suppose que les données suivent une distribution normale pour être valides. En outre, on suppose que les valeurs extrêmes sont rares et qu’elles n’impacteront pas ou peu le résultat. Si la distribution est asymétrique, il est préférable d’utiliser un t-test ordinal (comme une échelle de satisfaction par exemple, il n’y a pas d’écart fixe entre les valeurs) car celui-ci est plus robuste.
En revanche, pour les grands échantillons, les données extrêmes ont peu d’impact sur les résultats. De plus, il est possible d’identifier ces données à l’aide d’un autre outil de Tukey, il s’agit du Tukey’s Fence. En identifiant ces données, il est possible de les exclure si elles faussent les résultats ou bien de les garder puisqu’elles peuvent refléter une réalité sans troubler les résultats.

Réaliser une analyse de variance avec Selvitys

Réaliser une analyse de variance avec Selvitys
CE QU’IL FAUT RETENIR :
ANOVA, un outil statistique indispensable ?
L’analyse de variance est un outil statistique incontournable pour comparer plusieurs groupes et identifier des différences significatives. Ses différentes déclinaisons, à un facteur, deux facteurs et à mesures répétées, s’adaptent à une grande variété d’analyse.
Cependant, son interprétation nécessite une attention particulière, notamment due au flou qu’elle peut laisser. C’est pourquoi l’ANOVA est souvent accompagnée d’autres tests statistiques pour compléter son analyse. Bien utilisée, elle permet de tirer des conclusions solides et d’optimiser la prise de décision dans de nombreux domaines, de la recherche scientifique à l’étude marketing.


Selvitys : La solution idéale pour interroger vos clients
Selvitys met à votre disposition une plateforme complète pour créer, diffuser et analyser vos sondages en ligne, couvrant ainsi l’ensemble de vos besoins en études. Grâce à notre méthode de diffusion, nous sommes en mesure de recueillir plus de 1 000 réponses en moins de 24 heures auprès de notre panel qualifié.
Nous vous accompagnons dans le choix de la méthodologie la plus adaptée à votre projet, afin de garantir des résultats pertinents. En nous confiant votre sondage, vous bénéficiez d’une gestion clé en main : de la rédaction du questionnaire à la diffusion, jusqu’à l’analyse des données. Une fois toutes les réponses collectées, nous organisons un échange d’une heure pour vous assurer une parfaite compréhension des résultats et vous aider à affiner votre plan d’action. Un vrai gain de temps et d’efficacité !
Nos autres articles qui peuvent vous intéresser !
Méthode des quotas : le guide pour garantir la représentativité de vos sondages
Dans un environnement économique où la donnée pilote désormais chaque décision stratégique, la question de la fiabilité de vos sondages est devenue centrale. Qu’il s’agisse de valider le lancement d’un nouveau produit, d’ajuster une stratégie tarifaire ou de mesurer la santé de votre image de marque, la crainte de s’appuyer sur un échantillon « à côté de la plaque » est réelle.
Effet de halo : Comment éviter ce biais cognitif qui fausse vos études de marché ?
Alors que la donnée est devenue le moteur de toute décision stratégique, la fiabilité de vos études constitue désormais votre actif le plus précieux. Pourtant, une ombre plane systématiquement sur la précision de vos résultats, ce sont les biais cognitifs.
Test de logo : Le guide pour avoir un logo de marque parfait
L’identité visuelle est la pierre angulaire de votre stratégie de marque. Or, le choix d’un logotype repose trop souvent sur des préférences esthétiques subjectives en interne, plutôt que sur des données objectives. Pourtant, le logo représente la façade de votre marque.